强连通的定义是:有向图 G 强连通是指,G 中任意两个结点连通。
强连通分量(Strongly Connected Components,SCC)的定义是:极大的强连通子图。
Tarjan算法
对于一个连通块,以任意节点作为根节点进行深度优先搜索(DFS)。将节点的深度优先搜索序记为 dfn[x],将节点能够通过返祖边到达的最早节点的深度优先搜索序记为 low[x] 。若 low[x] 等于 dfn[x] ,则节点 x 为一个强连通分量的根。在进行深度优先搜索的同时,使用一个栈记录访问的节点,即可找出该强连通分量的所有节点。
vector<int> v[10005];
int dfn[10005], low[10005], scc[10005],pos, tot;
bool p[10005];//标记节点是否在栈中
stack<int> st;
void tarjan(int x) {
pos++;
dfn[x] = pos;
low[x] = pos;
st.push(x);
p[x] = true;
for (int i: v[x]) {
if (!dfn[i]) {
tarjan(i);
low[x] = min(low[x], low[i]);//在回溯过程中,用 low[i] 更新 low[x] 。因为存在从 x 到 i 的直接路径,所以 i 能够回溯到的已经在栈中的结点,x 也一定能够回溯到。
} else if (p[i])low[x] = min(low[x], dfn[i]);// i 被访问过,已经在栈中:根据 low 值的定义,用 low[i] 更新 low[x]。
}
if (low[x] == dfn[x]) {
tot++;//强连通分量的数量
scc[x] = tot;
p[x] = false;
while (st.top() != x) {
scc[st.top()] = tot;// scc 标记节点在哪个强连通分量中
p[st.top()] = false;
st.pop();
}
st.pop();
}
}由于可以多次经过一条边和一个点,并且点权为正,因此对于任意一个强连通分量,我们都可以先将所有点走一遍,再从任意一条路径走出。因此可以先缩点,同时记录每个强连通分量的点权和。再用拓扑进行 dp ,就可以求出最长路径。
#include<bits/stdc++.h>
#define int long long
using namespace std;
struct E {
int u, v;
};
vector<E> e;
vector<int> v[10005], r[10005];
int f[10005], ind[10005], a[10005], dfn[10005], low[10005], scc[10005], sum[10005], pos, tot;
bool p[10005];
stack<int> st;
void tarjan(int x) {
pos++;
dfn[x] = pos;
low[x] = pos;
st.push(x);
p[x] = true;
for (int i: v[x]) {
if (!dfn[i]) {
tarjan(i);
low[x] = min(low[x], low[i]);
} else if (p[i])low[x] = min(low[x], dfn[i]);
}
if (low[x] == dfn[x]) {
tot++;
scc[x] = tot;
p[x] = false;
sum[tot] = a[x];
while (st.top() != x) {
scc[st.top()] = tot;
sum[tot] += a[st.top()];
p[st.top()] = false;
st.pop();
}
st.pop();
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
e.push_back({x, y});
v[x].push_back(y);
}
for (int i = 1; i <= n; i++)if (!dfn[i])tarjan(i);
for (E i: e) {
int x = i.u, y = i.v;
if (scc[x] != scc[y]) {
r[scc[x]].push_back(scc[y]);
ind[scc[y]]++;
}
}
deque<int> q;
for (int i = 1; i <= tot; i++) if (ind[i] == 0)q.push_back(i);
int ans = 0;
while (!q.empty()) {
int u = q.front();
q.pop_front();
f[u] = max(f[u], sum[u]);
if (r[u].empty()) ans = max(ans, f[u]);
for (int i: r[u]) {
f[i] = max(f[i], f[u] + sum[i]);
ind[i]--;
if (ind[i] == 0)q.push_back(i);
}
}
cout << ans << '\n';
}对于第一个问题,很明显只要求出所有强连通分量的最大 size 即可。
对于第二个问题,我们首先将所有强连通分量缩成一个点,然后考虑如何加边才能使得所有点连通。
对于一个有向图,若每个节点入度和出度均不为 0 ,则该图强连通:
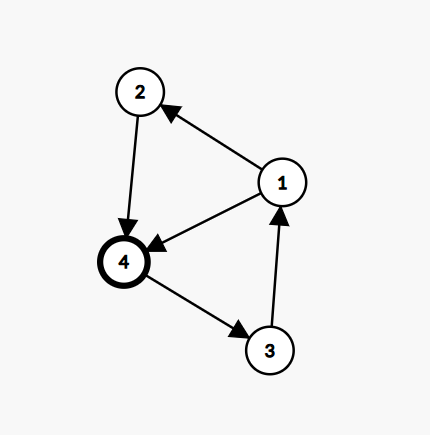
那么假如缩点后有节点(这里的节点即强连通分量)的入度或出度为 0 ,我们添加相应的入边或出边即可。由此可以想到,我们可以从出度为 0 的点连边到入度为 0 的点,例如下图。节点 3 的出度为 0 ,节点1 的入度为 0 ,那么连一条 3->1 边即可使整张图连通:
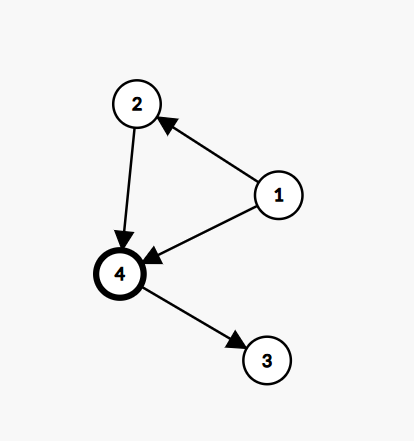
由此可得,若入度为 0 的点的数量为 CntIn ,出度为 0 的点的数量为 CntOut ,第二问答案即为 max(CntIn,CntOut) 。
特别地,若缩点后只有一个点,答案为 0 。
#include<bits/stdc++.h>
#define int long long
constexpr int N = 100005;
using namespace std;
struct E {
int u, v;
};
vector<E> e;
vector<int> v[N];
int ind[N], outd[N], dfn[N], low[N], scc[N], pos, tot, maxsize = 0;
bool p[N];
stack<int> st;
void tarjan(int x) {
pos++;
dfn[x] = pos;
low[x] = pos;
st.push(x);
p[x] = true;
for (int i: v[x]) {
if (!dfn[i]) {
tarjan(i);
low[x] = min(low[x], low[i]);
} else if (p[i])low[x] = min(low[x], dfn[i]);
}
if (low[x] == dfn[x]) {
tot++;
scc[x] = tot;
p[x] = false;
int sz = 1;
while (st.top() != x) {
scc[st.top()] = tot;
sz++;
p[st.top()] = false;
st.pop();
}
st.pop();
maxsize = max(maxsize, sz);
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
e.push_back({x, y});
v[x].push_back(y);
}
for (int i = 1; i <= n; i++)if (!dfn[i])tarjan(i);
for (E i: e) {
int x = i.u, y = i.v;
if (scc[x] != scc[y]) {
ind[scc[y]]++;
outd[scc[x]]++;
}
}
int in = 0, out = 0;
for (int i = 1; i <= tot; i++) {
if (ind[i] == 0)in++;
if (outd[i] == 0)out++;
}
int ans = tot == 1 ? 0 : max(in, out);
std::cout << maxsize << "\n" << ans << '\n';
}由于存在依赖关系并且可能有环,我们必须先对环进行处理。因为环上各点相互依赖,所以它们要么全部选,要么全部不选,因此可以直接缩点并将 W 和 V 相加。缩点后进行树上背包即可。
#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
constexpr int N = 105, M = 505;
int ind[N], W[N], w[N], A[N], a[N], dfn[N], low[N], scc[N], f[N][M], pos, tot, n, m;
bool p[N];
stack<int> st;
vector<int> v[N], V[N];
vector<pair<int, int>> e;
void tarjan(int x) {
pos++;
dfn[x] = pos;
low[x] = pos;
st.push(x);
p[x] = true;
for (int i: V[x]) {
if (!dfn[i]) {
tarjan(i);
low[x] = min(low[x], low[i]);
} else if (p[i])low[x] = min(low[x], dfn[i]);
}
if (low[x] == dfn[x]) {
tot++;
scc[x] = tot;
p[x] = false;
w[tot] = W[x];
a[tot] = A[x];
while (st.top() != x) {
scc[st.top()] = tot;
p[st.top()] = false;
w[tot] += W[st.top()];
a[tot] += A[st.top()];
st.pop();
}
st.pop();
}
}
void dfs(int x, int fa = -1) {
for (int i = w[x]; i <= m; i++) {
f[x][i] = a[x];
}
for (int i: v[x]) {
if (i == fa)continue;
dfs(i, x);
for (int j = m; j >= w[x]; j--) {
for (int k = 0; k <= j - w[x]; k++) {
f[x][j] = max(f[x][j], f[x][j - k] + f[i][k]);
}
}
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++)cin >> W[i];
for (int i = 1; i <= n; i++)cin >> A[i];
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
if (x) {
e.emplace_back(x, i);
V[x].push_back(i);
}
}
for (int i = 1; i <= n; i++) {
if (!dfn[i])tarjan(i);
}
for (auto i: e) {
int x = i.first, y = i.second;
if (scc[x] != scc[y]) {
v[scc[x]].push_back(scc[y]);
ind[scc[y]]++;
}
}
for (int i = 1; i <= tot; i++) {
if (!ind[i])v[0].push_back(i);
}
dfs(0);
int ans = 0;
for (int i = 0; i <= m; i++)ans = max(ans, f[0][i]);
cout << ans << '\n';
}