基环树指的是具备 n 个节点与 n 条边的连通图,存在并且仅存在一个环。
有关基环树的问题通常依照寻找环 -> 将环拆解为 n 棵子树,分别进行遍历 -> 单独对环上的各个点进行判断的顺序予以求解,以下述题目为例。
题目大意
给出一个基环树的n条边,求过每个点的最长简单路径长度。
样例输入
2
5
2 1
3 2
4 2
5 4
3 4
6
2 1
3 1
4 3
5 3
6 3
6 5样例输出
4 4 4 3 4 4
4 4 4 4 4 解题思路
我们先考虑在普通树下如何求解此类问题。
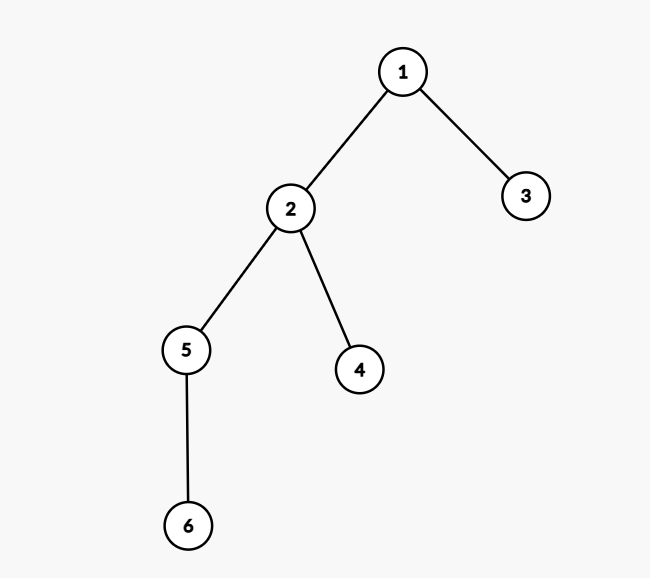
在树中,过某个节点的最长简单路径无非是两种情况:该点向下走的最长链+次长链,或该点向下走的最长链+向上走的最长链。以上图的节点 2 为例,经过 2 的最长简单路径由 2 – 4 – 6 和 2 – 1 – 3组成。
所以求解方法就很简单了,假设我们设maxd[i]为i节点向下走的最长链长度,maxu[i]为向上走的最长链长度,那么我们只需要做两遍DFS。第一遍,求出maxd和第一类答案;第二遍,求出maxu(maxu可由maxd向下传递得到)和第二类答案,与第一类答案进行比较。
在基环树中,上述方法是否仍然有效?
我们将样例中第二组数据的图画出如下:
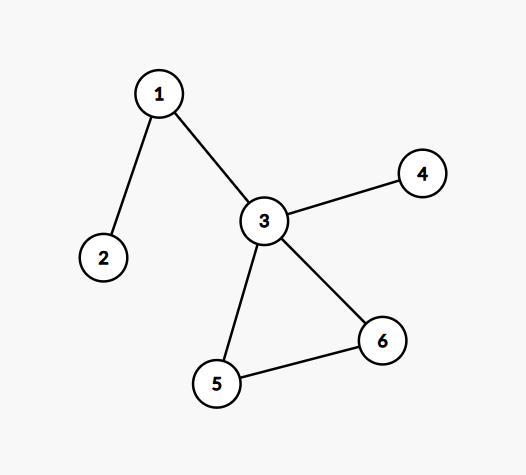
显然,对于不在环上的节点而言,此方法仍然有效,因为过这些节点的最长简单路径还是只有上述两种情况。但对于环上的节点而言,可能有第三种情况(例如过节点 5 的最长简单路径为 2 – 1 – 3 – 5 – 6,6并不在以 5 为根的子树上),此处暂时先不做考虑。
首先我们先将环找出(注意需要按顺序存,例如 3 – 6 – 5 ,方便后续计算),那么 maxd 就可以通过对每个环上点为根子树做一遍 DFS 求出。最后的难点在于如何求出环上点的 maxu 。
通过观察,我们可以很容易地看出,对于环上的一个节点 i ,maxu[i] = max { maxd[j] + dist[i , j] },其中 j 在环上,dist 表示 i 到 j 在环上的最长距离。显然,若我们对于每个 i 都枚举一个最大的 j ,时间复杂度就会来到 O( n² ) ,不可接受。
滑动窗口优化
考虑将环拆开并复制,可以得到一个序列,以上图为例,则为 3 5 6 3 5 6 (不唯一)。在这个序列上做距离前缀和 pre ,我们可以将上式修改为 maxu[i] = max{maxd[j] + pre[i] – pre[j] } 。由于 pre[i] 固定,将其提出,式子变为 maxu[i] = pre[i] + max{ maxd[j] – pre[j] } ,由于此题边权为 1 ,距离前缀和可以简化为下标,因此上式进一步化简为 maxu[i] = i + max{ maxd[j] – j } ,用一个大小为 tot (边上的点数)的滑动窗口维护 maxd[j] – j 的最大值即可。
注意到反方向的距离应该与正方向分开计算,即 tot – ( i – j ) 。上式变为maxu[i] = max{ maxd[j] + tot + j } – i 。再用一个滑动窗口维护 maxd[j] + tot + j 的最大值即可。
环上的第三类情况
我们画一棵更大的基环树。
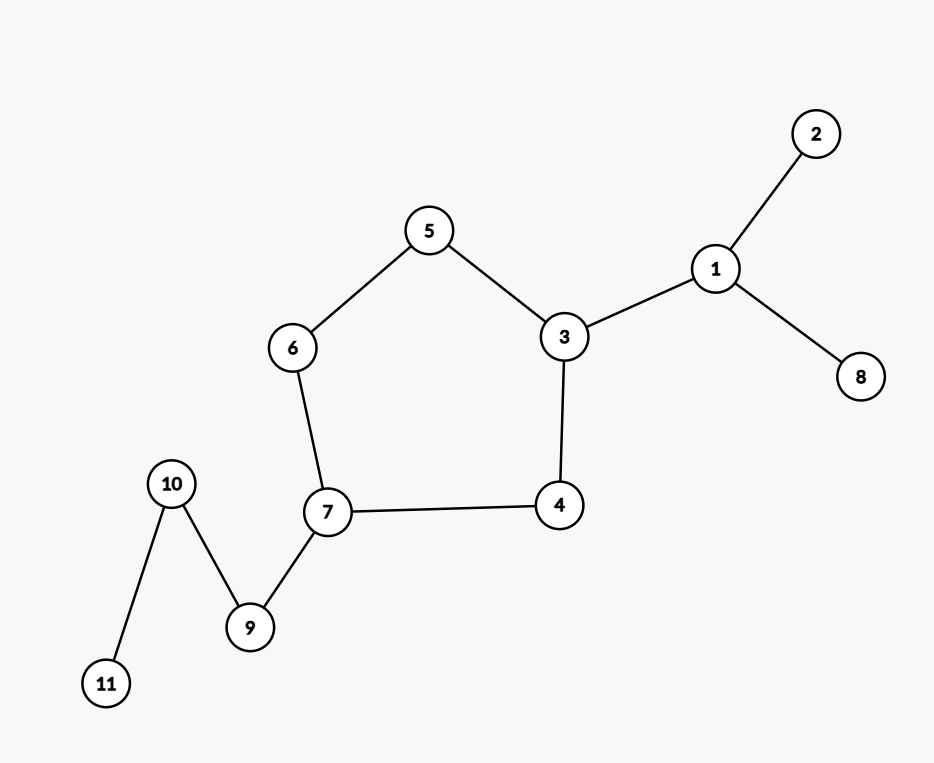
对于节点 5 ,他的子树大小为 1 ,因此 maxd[5] = 0 。他的最长简单路径由节点 7 的子树、节点 3 的子树以及 7 到 3 的环上路径组成。对于这种情况,我们可以考虑在上面求 maxu 的时候,记录正反方向最大值分别是由哪个 j 取得的,那么我们就可以得到两类 [i,j] :
第一类:途径节点 i ~ j 。
第二类:途径起点 ~ i 和 j ~ 终点。
那么我们显然可以用三个堆来维护上面的三段,求出第三类情况的答案,与前两类答案比较。
