题目背景

NOIP2013 普及组 T4

题目描述

一条单向的铁路线上，依次有编号为 1, 2, …, n 的 n 个火车站。每个火车站都有一个级别，最低为 1级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 x，则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。
注意：起始站和终点站自然也算作事先已知需要停靠的站点。

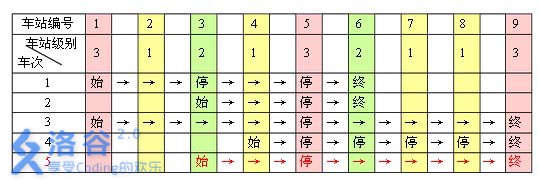
例如，下表是 5 趟车次的运行情况。其中，前 4 趟车次均满足要求，而第 5 趟车次由于停靠了 3 号火车站（2 级）却未停靠途经的 6 号火车站（亦为 2 级）而不满足要求。

现有 m 趟车次的运行情况（全部满足要求），试推算这 n 个火车站至少分为几个不同的级别。

输入格式

第一行包含 2 个正整数 n, m，用一个空格隔开。

第 i + 1 行 (1 ≤ i ≤ m) 中，首先是一个正整数 s_i (2 ≤ s_i ≤ n)，表示第 i 趟车次有 s_i 个停靠站；接下来有 s_i 个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式

一个正整数，即 n 个火车站最少划分的级别数。

样例 #1

样例输入 #1

9 2 
4 1 3 5 6 
3 3 5 6

样例输出 #1

2

样例 #2

样例输入 #2

9 3 
4 1 3 5 6 
3 3 5 6 
3 1 5 9

样例输出 #2

3

提示

对于 20% 的数据，1 ≤ n, m ≤ 10；

对于 50% 的数据，1 ≤ n, m ≤ 100；

对于 100% 的数据，1 ≤ n, m ≤ 1000。

思考

根据题目大意，自然地理解题目所给条件。以样例1为例，已知1 3 5 6比2 4高，3 5 6比2 4高，求车站的最小等级，如此明显的层级关系自然想到拓扑。以大小关系建图，大的指向小的，而后求整个图的层数。

代码

#include<iostream>
#include<vector>
#include<deque>
#include<algorithm>

using namespace std;
int inDegree[1001], level[1001], a[1001], ans = 0;
bool p[1001], pp[1001][1001];
vector<int> road[1001];
deque<int> q;

int main() {
    int n, m;
    cin >> n >> m;
    while (m--) {
        int x;
        cin >> x;
        for (int i = 1; i <= x; i++) {
            cin >> a[i];
            p[a[i]] = true;
        }
        for (int i = a[1]; i <= a[x]; i++) {
            if (!p[i]) {
                for (int j = 1; j <= x; j++) {
                    if (!pp[a[j]][i]) {
                        road[a[j]].push_back(i);
                        inDegree[i]++;
                        pp[a[j]][i] = true;
                    }
                }
            }
        }
        for (int i = 1; i <= x; i++)p[a[i]] = false;
    }
    for (int i = 1; i <= n; i++)if (inDegree[i] == 0)q.push_back(i);

    while (!q.empty()) {
        int temp = q.front();
        q.pop_front();
        for (int i = 0; i < road[temp].size(); i++) {
            inDegree[road[temp][i]]--;
            if (inDegree[road[temp][i]] == 0) {
                q.push_back(road[temp][i]);
                level[road[temp][i]] = level[temp] + 1;
                ans = max(ans, level[road[temp][i]]);
            }
        }
    }
    cout << ans + 1 << endl;
}